[n121] T-Test (One-Sample T-Test, Two-Sample T-Test, Chi-Square Test)

• One Sample t Test : 하나의 값과 하나의 집단 평균 검정
• Two Sample t Test : 두 집단 간 평균 검정
• Levene Test : 두 집단 간 분산 검정
• Chi^2 Test : 두 항목 간 독립 검정

 

One-Sample T-Test (일표본 평균 검정)

• 귀무 가설 : a값은 집단의 평균과 같다.
• 대립 가설 : a값은 집단의 평균과 다르다.

df1은 다음과 같을 때, 멤버십 계약을 한 사람들의 평균 가격이 전체 평균 가격과 같은지 비교해 보자.

 

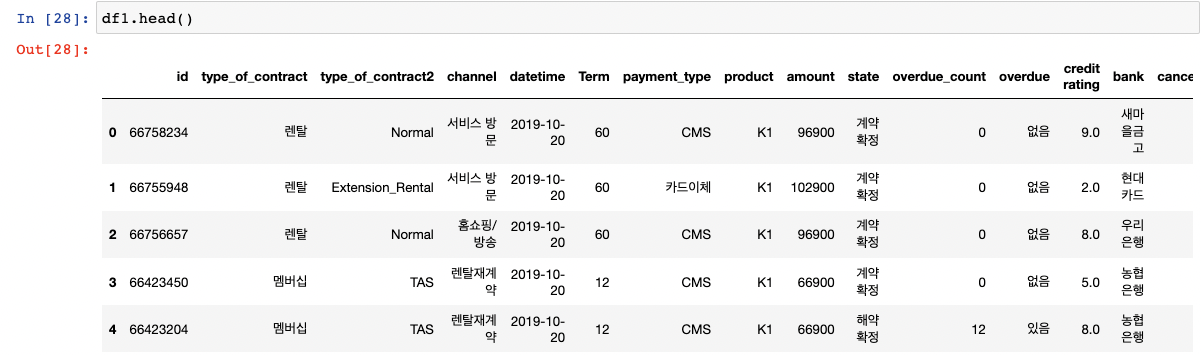
cond1 = (df1['type_of_contract'] == '멤버십')
df1_member = df1.loc[cond1]

# 귀무가설 : 96900원은 멤버십 집단의 평균과 같다. 
# 대립가설 : 96900원은 멤버십 집단의 평균과 다르다. 

stats.ttest_1samp(df1_member['amount'], 96900)
# 96900원 전체 집단의 median 값

p.value < 0.05 (귀무가설 기각 -> 대립 가설 참) 

신뢰도가 95%라 할 때, 기각역은 0.05이다.

실제로 df1_member의 평균 가격이 어떤지 살펴보면,

df1_member['amount'].mean()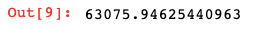

즉, 전체 집단 median 값이 96900과 크게 차이가 나는 것을 알 수 있다.

 

 

Two-Sample T-Test (이표본 평균 검정)

• 두 집단의 평균이 같냐, 다르냐를 판단하지만 수치가 정확하게 같은지를 보는 것은 아니다. 두 값의 차이가 통계적으로 유의미 한가 아닌가를 추정하는 테스트이다. 값이 완벽하게 같냐를 판단하는 것이 아님을 다시 한번 강조한다.
• 두 집단 평균의 차이가 있는지 검정
  • 귀무 가설 : 두 집단의 평균이 같다.
  • 대립 가설 : 두 집단의 평균이 다르다.
• 집단이 서로 등분산성을 보이지 않을 때 실시를 해준다. (즉, 두 집단 분산이 다를 때 실시)
  • Levene Test : 두 집단 분산의 차이가 있는지 검정 (대립 가설이 채택 될 때 -> two sample t test 실시 가능)
    • 귀무 가설 : 두 집단의 분산이 같다.
    • 대립 가설 : 두 집단의 분산이 다르다.

 

계약 유형에 따른 빈도수를 보자.

df1['type_of_contract'].value_counts()

 

렌탈 유형의 데이터는 df1_rental, 멤버십 유형의 데이터는 df1_member 로 추출한다.

cond1 = (df1['type_of_contract'] == '렌탈')

df1_rental = df1.loc[cond1]
df1_member = df1.loc[~cond1].dropna()

 

 

두 집단의 분산이 다를 때 Two Sample T-Test를 실시 할 수 있으므로, 분산을 비교하자.

두 집단의 등분산 검정

• 귀무 가설 : 렌탈 그룹과 멤버십 그룹의 amount 값의 분산의 차이가 없다.
• 대립 가설 : 렌탈 그룹과 멤버십 그룹의 amount 값의 분산의 차이가 있다.

stats.levene(df1_rental['amount'], df1_member['amount'])

 

p.value < 0.04 (귀무 가설 기각, 대립 가설 참)
렌탈 그룹과 멤버십 그룹의 amount 값의 분산 차이가 있다.

단순 계산해서 분산을 확인해 보자.

print(df1_rental['amount'].var())
print(df1_member['amount'].var())

144928790.0446055

14989768.519928247

실제로 두 집단의 분산은 크게 차이가 난다. 

 

이제 이표본 평균 검정을 실시한다.

# 이표본 평균검정
# 귀무 가설 : 렌탈그룹과 멤버십 그룹의 amount 평균값의 차이가 없다.
# 대립 가설 : 렌탈그룹과 멤버십 그룹의 amount 평균값의 차이가 있다.

stats.ttest_ind(df1_rental['amount'], df1_member['amount'])

p.value < 0.05 (귀무 가설 기각, 대립 가설 참)
대립 가설 : 렌탈그룹과 멤버십 그룹의 amount 평균값의 차이가 있다.

단순 계산으로 다시 한번 확인 할 수 있다.

print(df1_rental['amount'].mean())
print(df1_member['amount'].mean())

97200.31561283105

67100.63882063882

 

---

 

One-Sample Chi-Square Test

• 데이터의 분포가 예상과 같나.
• 귀무 가설 : 데이터의 분포가 a와 같다. 
• 대립 가설 : 데이터의 분포가 a와 다르다.

v1 = [18,22,20,15,23,22]
v2 = [5,23,26,19,24,23]

def myChisq(value):
  return print(stats.chisquare(value))

myChisq(v1)

 

 

 

Two-Sample Chi-Square Test

• 두 범주형 집단의 독립성 검정 (서로 연관이 있나 없나)
• 귀무 가설 : a항목과 b 항목은 서로 독립적이다. (연관성 없다)
• 대립 가설 : a항목과 b 항목은 서로 의존적이다. (연관성 있다)

 

Contingency Table (빈도 테이블)

df1_crosstable = pd.crosstab(df1['type_of_contract'], df1['product'])
df1_crosstable

 

• 귀무 가설 : 계약 유형에 따라 product의 차이가 없다. (계약유형과 product는 서로 독립)
• 대립 가설 : 계약 유형에 따라 product의 차이가 있다. (계약유형과 product는 서로 연관)

stats.chi2_contingency(df1_crosstable)
# 9.218461328024673e-288 이 pvalue

 pvalue = 9.218461328024673e-288 으로 출력되었다.

• p.value < 0.05 (귀무 가설 기각, 대립 가설 참)
• 계약 유형에 따라 product의 차이가 있다. (계약유형과 product는 서로 연관)

 

다음 영상을 참고하며 공부하였다. 매우 매우 강추하는 강의! 

 

 

 

총 정리

	무엇을 판단	One-sample	Two-sample
T-test	평균	귀무 가설 : A 값은 평균과 같다. stats.ttest_1samp(df, A)	귀무 가설 : 두 집단의 평균이 같다. stats.ttest_ind(df_1, df_2)
Chi-Square Test	분산	귀무 가설 : 데이터가 균등한 분포이다. stats.chisquare(df) 귀무 가설 : 집단의 분산이 예상 a와 같다. stats.chisquare(df, a)	귀무 가설 : 두 집단은 서로 독립적이다. stats.chi2_contingency(df)

 

 

부트캠프 공부 내용 한 눈에 보기

[인덱스] 코드 스테이츠 AI 부트캠프