[n121] 가설 검정 (t-test)

가설 검정이란

주어진 가설을 수치적으로 확인하는 프로세스이다. 

 

기술 통계치  (Descriptive Statistics)

[개념 통계 06] 기술 통계와 추리 통계란 무엇인가?

수집한 데이터를 설명/요약하는 통계치를 기출 통계치라고 한다. 예를 들어 count, mean, standard dev, min, max, 1Q, 2Q, 3Q, median 값 등이 있다. Summary Statistics라고도 부른다.

 

기술 통계치의 시각화

데이터를 이해하기 쉽게 하기 위해 시각화 한다.

• Boxplot

 

• Bagplot : 여러개의 features 들에 대한 그래프 (난해해서 잘 안 쓰인다)

 

• Violinplot

 

데이터의 기술 통계 찾는 코드

import pandas as pd
df = pd.DataFrame({'a': [1,2,3,4,5], 'b': [2,4,6,8,10]})
df.describe()

 

 

추리 통계치 (Inferential Statistics)

전수 조사를 한 데이터가 있으면 좋다. 하지만, 비용 / 시간 등의 이유로 전수 조사하기 어려운 경우가 있다. 그래서 전체 집단의 일부만 조사하여 데이터를 만든다. 샘플을 이용하여 모집단의 평균 등을 구할 수 있다.

 

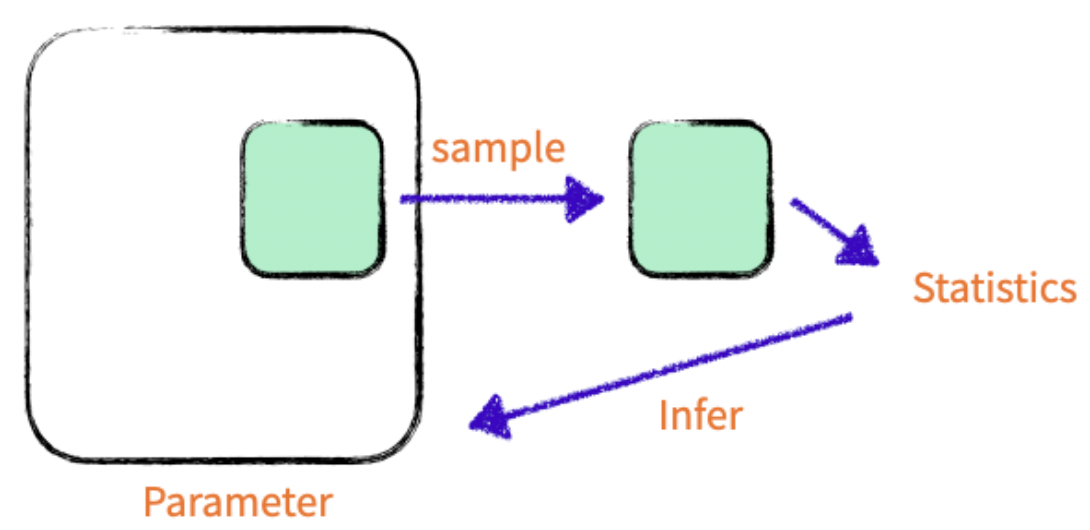
Effective Sampling

효과적으로 샘플을 추출하기 위한 방법들이 있다.

• Simple Random Sampling : 무작위 추출
• Systematic Sampling : 규칙을 가지고 추출.
• Stratified Random Sampling : 모집단을 그룹으로 나누고, 그 그룹 내에서 무작위 추출.
• Cluster Sampling : 모집단을 여러 그룹으로 나누고, 그룹 하나만 선택하여 추출. 

 

 

가설 검정

주어진 상황에 대해, 설정한 가설이 맞는지 아닌지 판단하는 과정. 

np.random.seed(1111) 
# binomial은 동전 앞면과 뒷면 처럼 2가지의 경우의 수만 있을 경우 쓴다
# 베르누이 분포라고 부른다
# 한 개의 동전이 앞면과 뒷면이 나올 확률이 반 반 일 때 (p=0.5), 총 10번 던져라.
df = pd.DataFrame({'coinflips': np.random.binomial(n = 1, p = 0.5, size = 10)})

df.hist();

 

표본 평균의 표준 오차 ( Standard Error of the Sample Mean )

에러를 수치화 한다. 

에러는 샘플의 표준 편차 / root(표본의 수)

즉, 표본의 수가 많아질 수록 에러는 작아진다. 

 

Student T-test

크게 두 종류가 있다. One Sample t-test, Two Sample t-test.

One Sample t-test

샘플데이터의 평균값이 특정한 값과 같은지 아닌지 비교한다. 

t = (샘플 데이터의 평균 - 비교 하고자 하는 값) / (에러)

 

T-test Process

1.  귀무 가설 (Null Hypothesis)를 설정

2. 대안 가설 (Alternative Hypothesis)를 설정

3. 신뢰도를 설정 (Confidence Level) : 보통 95%, 99% 설정

신뢰도 95% = 모수가 신뢰 구간 안에 포함될 확률이 95% = 귀무가설이 틀렸지만 우연히 성립할 확률이 5%

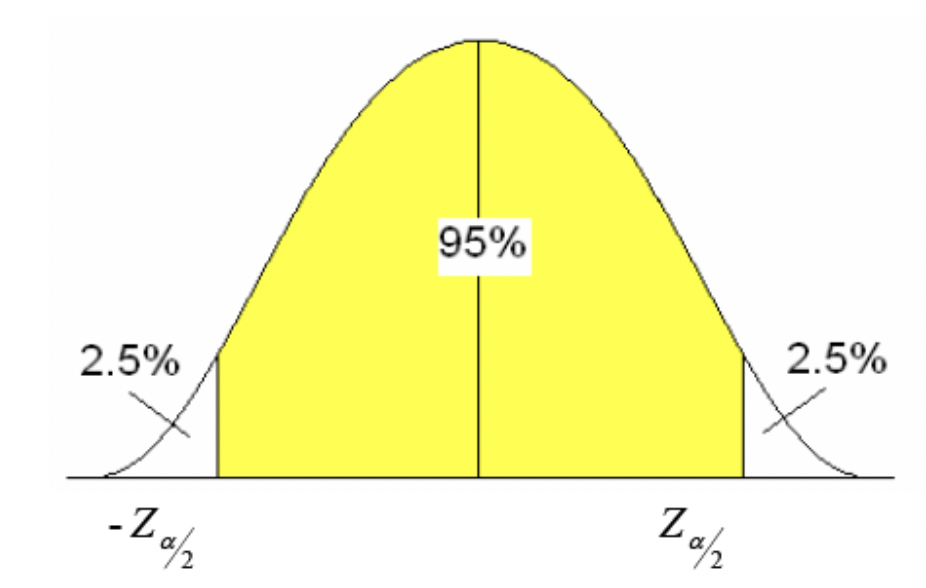
4. P-value 확인

주어진 가설이 통계적으로 얼마나 유의한가를 0에서 1 사이 값으로 지표한다. p-value가 낮다 = 귀무 가설이 틀릴 확률이 높다.

5. P-value를 기반으로 가설에 대한 결론

 

Scipy로 T-test 구현하기

scipy.stats.ttest_1samp — SciPy v1.7.1 Manual

 

P-value의 기준

1. pvalue < 0.01 : 귀무가설이 옳을 확률이 1%이하 -> 틀렸다 (깐깐한 기준)

2. pvalue < 0.05 (5%) : 귀무가설이 옳을 확률이 5%이하 -> 틀렸다 (일반적인 기준)

 0.05 ~ pvalue ~ 0.1 사이인 경우: (애매함)

• 실험을 다시한다.
• 데이터를 다시 뽑는다.
• 샘플링을 다시한다
• 기존의 경험 / 인사이트를 바탕으로 가설에 대한 결론을 내린다.

3. pvalue > 0.1 (10%) : 귀무가설이 옳을 확률이 10%이상인데 -> 귀무가설이 맞다 ~ 틀리지 않았을것이다

np.random.seed(1111)

coinflips = np.random.binomial(n = 1, p = 0.5, size = 1000)

print(np.mean(coinflips))

from scipy import stats

# ttest_1samp 함수의 파라미터 1) Sample 데이터, 2) 비교하려는 값

stats.ttest_1samp(coinflips, .5)

Out[9]:

Ttest_1sampResult(statistic=0.5690174909554405, pvalue=0.5694721717152109)

 

pvalue값이 낮은 예시

# 0.6을 기준으로 동전을 10번, 100번, 1000번 던질 때, 평균이 0.5인가?
print(stats.ttest_1samp(np.random.binomial(n = 1, p = 0.6, size = 10), .5))
print(stats.ttest_1samp(np.random.binomial(n = 1, p = 0.6, size = 100), .5))
print(stats.ttest_1samp(np.random.binomial(n = 1, p = 0.6, size = 1000), .5))

Ttest_1sampResult(statistic=1.3093073414159542, pvalue=0.22286835013352013) Ttest_1sampResult(statistic=1.8207158484808839, pvalue=0.07167088885580167) Ttest_1sampResult(statistic=5.8501734426276215, pvalue=6.650107077235998e-09)

즉, 세 번째 pvalue는 e-09 이므로 -> 아니다. 

e-1 은 0.1, e-2 은 0.01. 6.65e-09 = 0.00000000665

 

One-side test vs Two-side test

Two side (tail / direction) test : 샘플을 두 방향으로 고려해야 한다. 샘플 데이터의 평균이 "X"와 같다 / 같지 않다. 를 검정하는 내용

One side test : 샘플 데이터의 한 방향을 고려하면 된다. 샘플 데이터의 평균이 "X"보다 크다 혹은 작다 / 크지 않다 작지 않다. 를 검정하는 내용

 

Two Sample t-test

2개 샘플의 평균이 서로 동일한가 비교하는 방법. 

np.random.seed(111)

coin1 = np.random.binomial(n = 1, p = 0.5, size = 500)
coin2 = np.random.binomial(n = 1, p = 0.5, size = 200)

print(np.mean(coin1))
print(np.mean(coin2))

stats.ttest_ind(coin1, coin2)

 

 

t-value 

t-value를 검정 통계량으로 사용한다. 

두 표본 집단의 차이 / 두 그룹 간 평균 차이에 대한 불확실도

( 즉, 두 표본 집단의 차이 * 두 그룹 간 평균 차이에 대한 확실도 라고 생각하면 쉽다)

 

One-tailed test

기준 값보다 큰지 작은지 비교 한다. Alternative = 'greater', 'less' 사용한다.

예를 들어, 평균 느티나무 수와 평균 왕벚나무 수를 비교 하자. 

귀무 가설은 평균 왕벚나무 수가 느티나무 수보다 크다고 가정한다. 

반대로, 대립 가설은 '평균 느티나무 수가 왕벚나무 수보다 크다' 이다. 

 stats.ttest_ind(느티나무, 왕벚나무, alternative='greater')   이 경우 귀무 가설을 거절 -> 대립 가설 채택 되면 느티나무 수가 더 크다는 가설이 채택된다. 

귀무 가설이 채택 되기 위해서는 (p/2 < alpha and t < 0) 조건을 만족해야 하며,

대립 가설이 채택 되기 위해서는 (p/2 < alpha and t > 0) 조건을 만족해야 한다. 

# 귀무가설 : 평균 느티나무 수 > 평균 왕벚나무 수
# 대립가설 : 평균 느티나무 수 < 평균 왕벚나무 수

# (p/2 < alpha and t < 0) 라면, 귀무 가설 채택
# (p/2 < alpha and t > 0) 라면, 대립 가설 채택
# Alternative Hypothesis that you are trying to prove is that mean(second)>mean(first), 
# then you can call scipy.stats.ttest_ind(second, first)

# 귀무가설 판단의 기준이 p value 0.05 (변수 alpha 선언)
alpha = 0.05

stats.ttest_ind(trees_king, trees_neuti)
pv = stats.ttest_ind(trees_neuti, trees_king, alternative = 'greater').pvalue
tv = stats.ttest_ind(trees_neuti, trees_king, alternative = 'greater').statistic

def find_ans(pvalue):
  if ((pvalue/2 > alpha) & (tv < 0)):
    return print('왕벚나무')
  elif ((pvalue/2 < alpha) & (tv > 0)):
    return print('느티나무')
  else:
    return print('없음')

ans = find_ans(pv)
ans

 

How to perform two-sample one-tailed t-test with numpy/scipy

 

 

부트캠프 공부 내용 한 눈에 보기

[인덱스] 코드 스테이츠 AI 부트캠프