[회귀] Lidge/Lasso/ElasticNet

1  규제 선형 회귀 개요

• 비용 함수 목표는 RSS를 최소화 하는 것이 목표.
• 회귀 모델은 적절히 데이터에 적합하면서도 회귀 계수가 기하급수적으로 커지는 것을 제어해야 한다.

1.1  규제 선형 모델에서의 alpha의 역할

• alpha=0인 경우, w(회귀 계수)가 커도 alpha*w2가 0이 되어 비용 함수는 min(RSS)
• alpha=무한대인 경우, alpha*w2도 무한대가 되므로 비용 함수는 w를 0에 가깝게 최소화 해야 한다.

1.2  규제 선형 회귀의 유형

• 비용 함수에 alpha 값으로 페널티를 부여해 회귀 계수 값의 크기를 감소시켜서 과적합 개선.
• 규제는 L2, L1 방식.
• L2 규제를 적용한 회귀가 릿지 회귀
• L1 규제를 적용한 회귀가 라쏘 회귀. w의 절대값에 대해 패널티 부여. 영향력이 크지 않은 회귀 계수 값을 0으로 변환.
• ElasticNet : L2, L1 규제를 함께 결합한 모델. 피처가 많은 데이터 세트에 적용.

 

2  Ridge Regression

# 앞의 LinearRegression예제에서 분할한 feature 데이터 셋인 X_data과 Target 데이터 셋인 Y_target 데이터셋을 그대로 이용 
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
from sklearn.datasets import load_boston

# boston 데이타셋 로드
boston = load_boston()

# boston 데이타셋 DataFrame 변환 
bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names)

# boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함. 
bostonDF['PRICE'] = boston.target
print('Boston 데이타셋 크기 :',bostonDF.shape)

y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)


ridge = Ridge(alpha = 10)
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores  = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 3))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores,3))
print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))

Boston 데이타셋 크기 : (506, 14)
5 folds 의 개별 Negative MSE scores: [-11.422 -24.294 -28.144 -74.599 -28.517]
5 folds 의 개별 RMSE scores : [3.38 4.929 5.305 8.637 5.34 ]
5 folds 의 평균 RMSE : 5.518

 

2.1  alpha값을 0 , 0.1 , 1 , 10 , 100 으로 변경하면서 RMSE 측정

# Ridge에 사용될 alpha 파라미터의 값들을 정의
alphas = [0 , 0.1 , 1 , 10 , 100]

# alphas list 값을 iteration하면서 alpha에 따른 평균 rmse 구함.
for alpha in alphas :
    ridge = Ridge(alpha = alpha)
    
    #cross_val_score를 이용하여 5 fold의 평균 RMSE 계산
    neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
    avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
    print('alpha {0} 일 때 5 folds 의 평균 RMSE : {1:.3f} '.format(alpha,avg_rmse))

alpha 0 일 때 5 folds 의 평균 RMSE : 5.829
alpha 0.1 일 때 5 folds 의 평균 RMSE : 5.788
alpha 1 일 때 5 folds 의 평균 RMSE : 5.653
alpha 10 일 때 5 folds 의 평균 RMSE : 5.518
alpha 100 일 때 5 folds 의 평균 RMSE : 5.330

 

2.2  각 alpha에 따른 회귀 계수 값을 시각화. 각 alpha값 별로 plt.subplots로 맷플롯립 축 생성

# 각 alpha에 따른 회귀 계수 값을 시각화하기 위해 5개의 열로 된 맷플롯립 축 생성  
fig , axs = plt.subplots(figsize=(18,6) , nrows=1 , ncols=5)
# 각 alpha에 따른 회귀 계수 값을 데이터로 저장하기 위한 DataFrame 생성  
coeff_df = pd.DataFrame()

# alphas 리스트 값을 차례로 입력해 회귀 계수 값 시각화 및 데이터 저장. pos는 axis의 위치 지정
for pos , alpha in enumerate(alphas) :
    ridge = Ridge(alpha = alpha)
    ridge.fit(X_data , y_target)
    # alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.  
    coeff = pd.Series(data=ridge.coef_ , index=X_data.columns )
    colname='alpha:'+str(alpha)
    coeff_df[colname] = coeff
    # 막대 그래프로 각 alpha 값에서의 회귀 계수를 시각화. 회귀 계수값이 높은 순으로 표현
    coeff = coeff.sort_values(ascending=False)
    axs[pos].set_title(colname)
    axs[pos].set_xlim(-3,6)
    sns.barplot(x=coeff.values , y=coeff.index, ax=axs[pos])

# for 문 바깥에서 맷플롯립의 show 호출 및 alpha에 따른 피처별 회귀 계수를 DataFrame으로 표시
plt.show()

 

 

2.3  alpha 값에 따른 컬럼별 회귀계수 출력

ridge_alphas = [0 , 0.1 , 1 , 10 , 100]
sort_column = 'alpha:'+str(ridge_alphas[0])
coeff_df.sort_values(by=sort_column, ascending=False)

 

3  라쏘 회귀

• w의 절대값에 페널티를 부여하는 L1 규제를 선형 회귀에 적용한 것이 라쏘 회귀.
• L2 규제가 회귀 계수의 크기를 감소시키는데 반해, L1 규제는 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거.

from sklearn.linear_model import Lasso, ElasticNet

# alpha값에 따른 회귀 모델의 폴드 평균 RMSE를 출력하고 회귀 계수값들을 DataFrame으로 반환 
def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None, verbose=True):
    coeff_df = pd.DataFrame()
    if verbose : print('####### ', model_name , '#######')
    for param in params:
        if model_name =='Ridge': model = Ridge(alpha=param)
        elif model_name =='Lasso': model = Lasso(alpha=param)
        elif model_name =='ElasticNet': model = ElasticNet(alpha=param, l1_ratio=0.7)
        neg_mse_scores = cross_val_score(model, X_data_n, 
                                             y_target_n, scoring="neg_mean_squared_error", cv = 5)
        avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
        print('alpha {0}일 때 5 폴드 세트의 평균 RMSE: {1:.3f} '.format(param, avg_rmse))
        # cross_val_score는 evaluation metric만 반환하므로 모델을 다시 학습하여 회귀 계수 추출
        
        model.fit(X_data , y_target)
        # alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가. 
        coeff = pd.Series(data=model.coef_ , index=X_data.columns )
        colname='alpha:'+str(param)
        coeff_df[colname] = coeff
    return coeff_df
# end of get_linear_regre_eval

# 라쏘에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
lasso_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_lasso_df =get_linear_reg_eval('Lasso', params=lasso_alphas, X_data_n=X_data, y_target_n=y_target)

####### Lasso #######
alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.612
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.615
alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.669
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.776
alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.189

# 반환된 coeff_lasso_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(lasso_alphas[0])
coeff_lasso_df.sort_values(by=sort_column, ascending=False)

 

4  엘라스틱넷 회귀

# 엘라스틱넷에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
# l1_ratio는 0.7로 고정
elastic_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_elastic_df =get_linear_reg_eval('ElasticNet', params=elastic_alphas,
                                      X_data_n=X_data, y_target_n=y_target)

####### ElasticNet #######

alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.542

alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.526

alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.467

alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.597

alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.068

 

# 반환된 coeff_elastic_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(elastic_alphas[0])
coeff_elastic_df.sort_values(by=sort_column, ascending=False)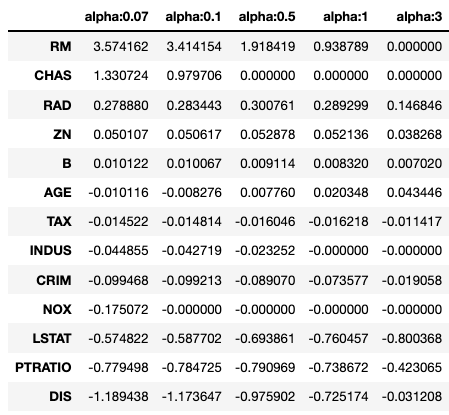

 

5  선형 회귀 모델을 위한 데이터 변환

from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures

# method는 표준 정규 분포 변환(Standard), 최대값/최소값 정규화(MinMax), 로그변환(Log) 결정
# p_degree는 다향식 특성을 추가할 때 적용. p_degree는 2이상 부여하지 않음. 
def get_scaled_data(method='None', p_degree=None, input_data=None):
    if method == 'Standard':
        scaled_data = StandardScaler().fit_transform(input_data)
    elif method == 'MinMax':
        scaled_data = MinMaxScaler().fit_transform(input_data)
    elif method == 'Log':
        scaled_data = np.log1p(input_data)
    else:
        scaled_data = input_data

    if p_degree != None:
        scaled_data = PolynomialFeatures(degree=p_degree, 
                                         include_bias=False).fit_transform(scaled_data)
    
    return scaled_data

# Ridge의 alpha값을 다르게 적용하고 다양한 데이터 변환방법에 따른 RMSE 추출. 
alphas = [0.1, 1, 10, 100]
#변환 방법은 모두 6개, 원본 그대로, 표준정규분포, 표준정규분포+다항식 특성
# 최대/최소 정규화, 최대/최소 정규화+다항식 특성, 로그변환 
scale_methods=[(None, None), ('Standard', None), ('Standard', 2), 
               ('MinMax', None), ('MinMax', 2), ('Log', None)]
for scale_method in scale_methods:
    X_data_scaled = get_scaled_data(method=scale_method[0], p_degree=scale_method[1], 
                                    input_data=X_data)
    print('\n## 변환 유형:{0}, Polynomial Degree:{1}'.format(scale_method[0], scale_method[1]))
    get_linear_reg_eval('Ridge', params=alphas, X_data_n=X_data_scaled, 
                        y_target_n=y_target, verbose=False)