[프로젝트] 게임 설계를 위한 데이터 분석

섹션 1 프로젝트는 다음 분기에 설계할 게임을 위해 게임 출고량 데이터를 분석하는 것이다.

사용된 데이터는 1980년부터 2016년까지의 게임 출고량 데이터셋입니다.

먼저, 연도별 게임 장르 트렌드 그래프를 보면 액션, 어드벤쳐, 롤플레잉, 슈팅, 스포츠 장르가 크게 인기를 끌었습니다.

 

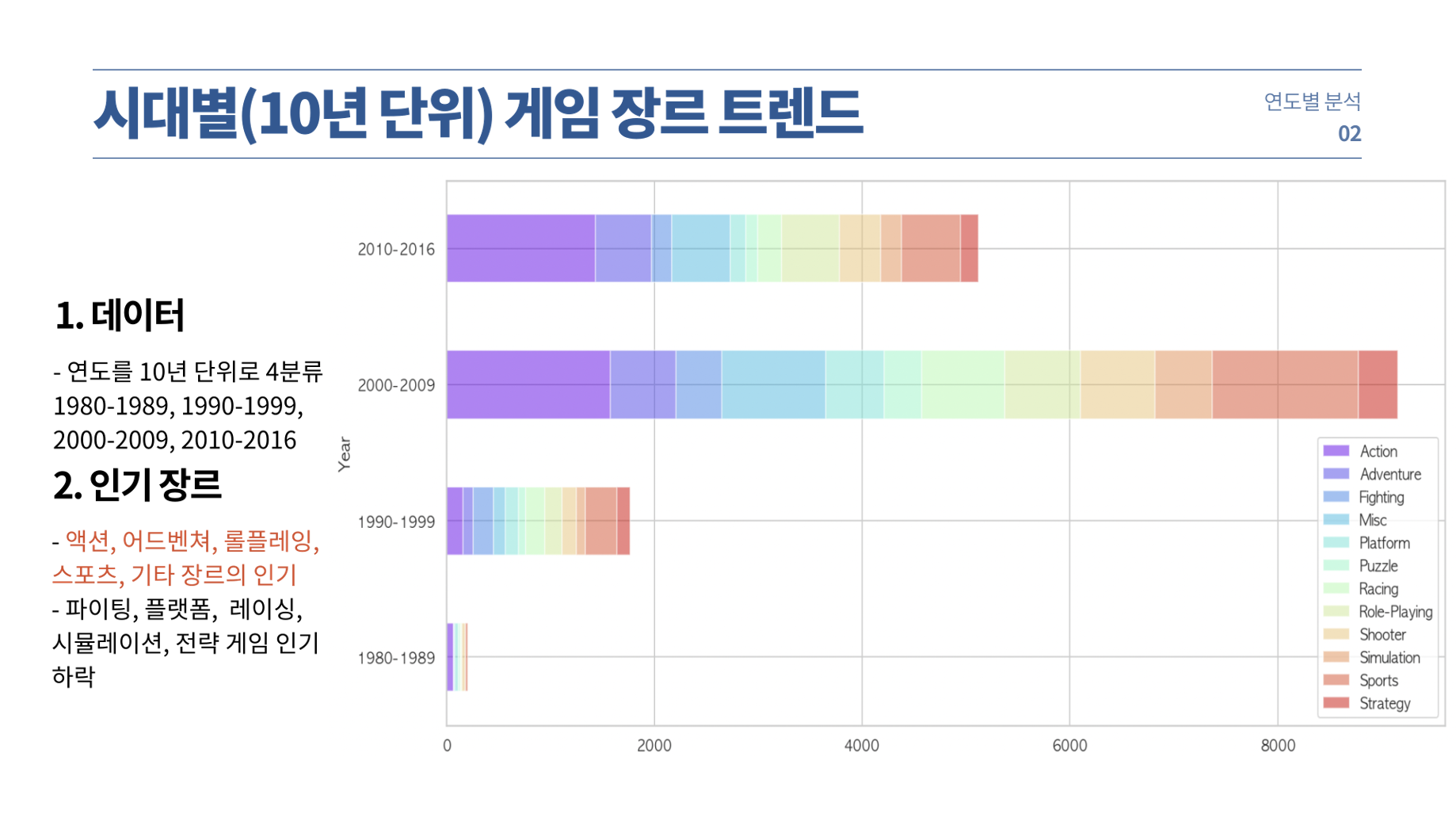
위 데이터의 연도를 10년 단위로 묶어, 네 분류로 나누었습니다.

파이팅, 플랫폼, 레이싱, 시뮬레이션, 전략 게임 출고량이 하락한 것을 확인할 수 있습니다.

 

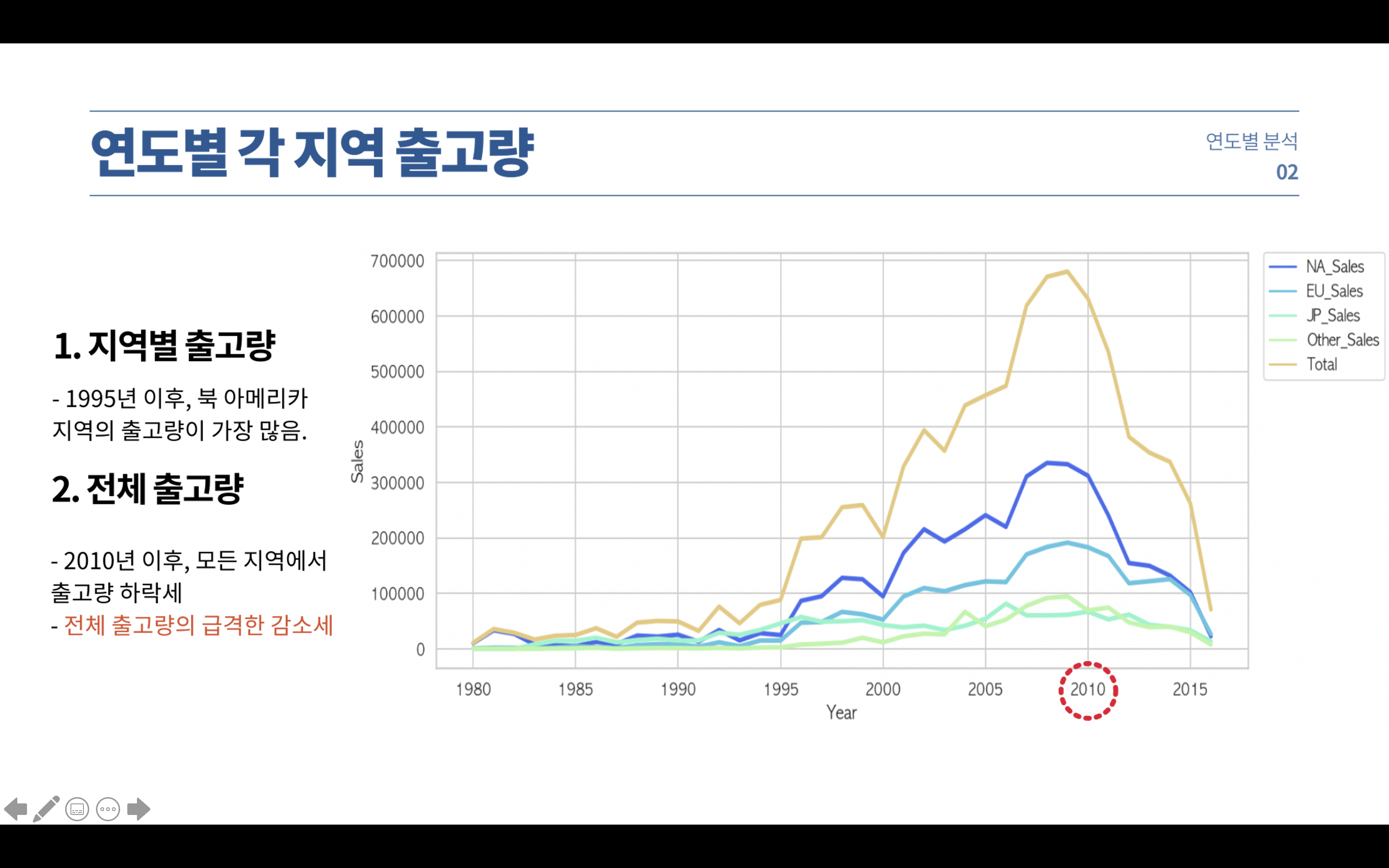
각 지역별로 게임 출고량을 봤을 때, 파란색인 북미와 하늘색 유럽 출고량이 가장 높습니다.

전체 데이터인 노란색을 보면,  2010년 전후로 크게 하락한 것을 확인할 수 있습니다.

 

급격하게 출고량이 감소하는 원인을 찾고자 넷플릭스 수익 데이터를 가져왔습니다.

파란색 바는 넷플릭스 수익, 빨간색 라인은 게임 출고량 입니다.

2010년 즈음부터 넷플릭스 수익이 크게 증가함과 동시에 게임 출고량이 급격하게 감소하는 것을 볼 수 있습니다.

이는 게임과 같이 대표적인 실내 엑티비티인 넷플릭스가 게임 출고량에 영향을 끼칠 수 도 있음을 시사합니다.

다음은, 출고량 수치에 따라 지도 위에 표시하였습니다.

가장 색이 짙은 북미에서 출고량이 높고, 그 다음은 유럽 시장에서 출고량이 높은 것을 볼 수 있습니다.

지역별 선호하는 게임 장르로는, 북미와 유럽 지역에서는 액션 게임이,

일본 지역에서는 롤플레잉 게임이 가장 인기가 많았습니다.

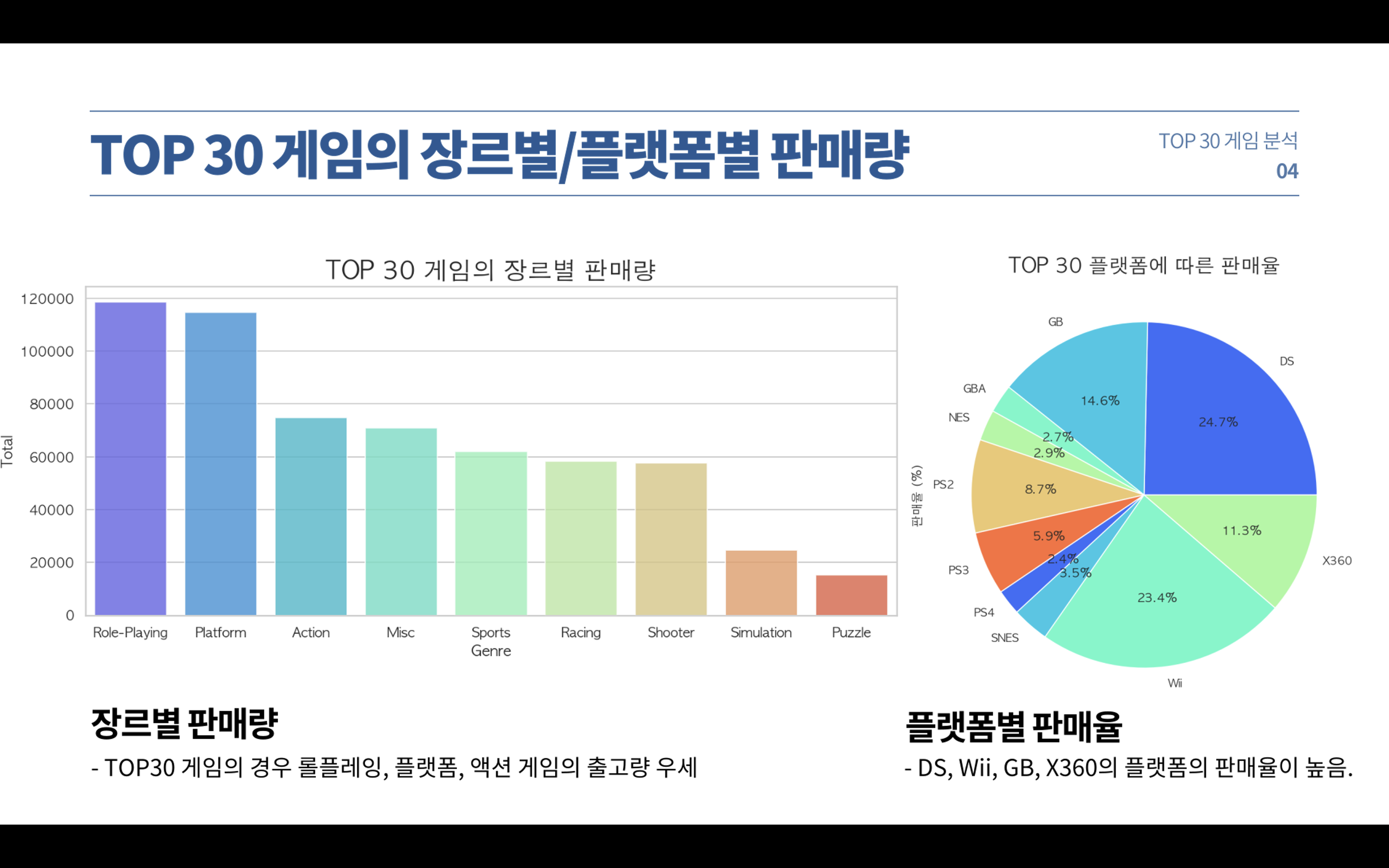
가장 출고량이 많은 탑30 게임 분석입니다.

전체 게임에서는 액션 장르가 인기가 많았지만 탑30에서는 롤플레잉 장르가 가장 출시량이 많았습니다.

플랫폼별 판매율은 Wii와 ds의 인기가 많습니다.

그렇다면, 게임 장르에 따라 출고량이 많은 플랫폼이 있을까 하는 의문점이 생겼습니다.

이를 위해, 독립성을 보여주는 카이 제곱 테스트를 시행하였고, 그 결과 pvalue가 0이 나왔습니다.

즉, 게임 장르와 플랫폼은 서로 연관성이 있다고 보여집니다.

위의 결과에 따라, 인기 많은 장르 여섯가지의 플랫폼별 출고량을 시각화하였습니다.

장르에 따라 각기 다른 플랫폼이 인기가 있는 것을 확인할 수 있습니다.

또한, 전체 데이터에서 게임 이름의 빈도수를 확인하기 위해 워드 클라우드를 사용하였습니다.

피파, NFL 등과 같이 스포츠 게임의 빈도수가 높은 것을 통해, 스포츠 게임이 시리지물로 제작되는 경우가 많음을 알 수 있습니다.

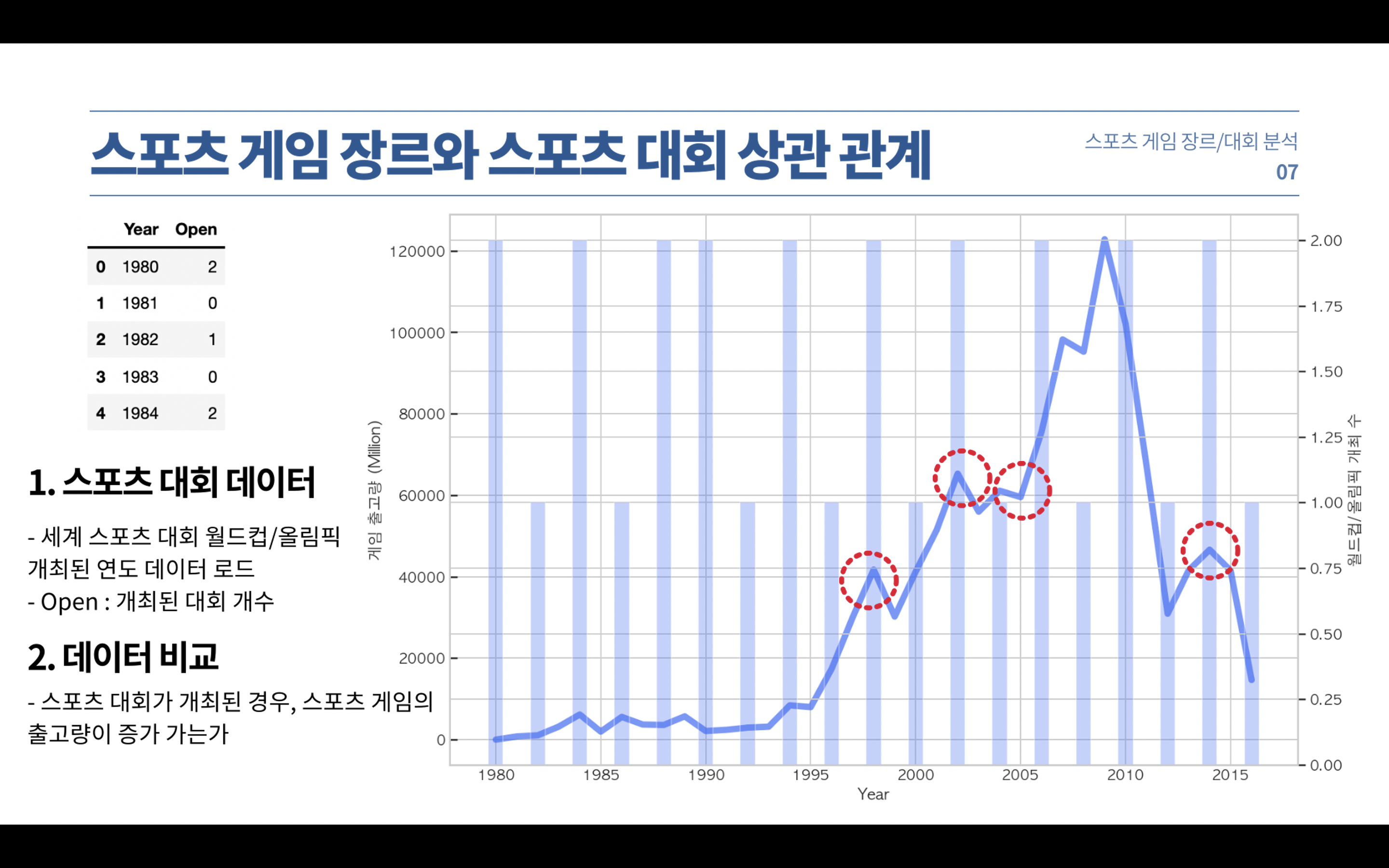
그렇다면, 세계 스포츠 대회가 스포츠 게임 장르 출고량에 영향을 끼칠까? 라는 의문이 또 생깁니다.

하늘색 바는 그 해에 개최된 월드컵/올림픽 대회 개수이며,

파란색 라인은 스포츠 게임 장르의 출고량입니다.

스포츠 대회가 개최된 해에는 출고량이 급증하는 것처럼 보입니다. 

확인하기 위해, 스포츠 대회 개최 횟수와 스포츠 게임 츨고량 데이터를 크로스 테이블 하였습니다.

다음과 같이 pvalue가 0.41이므로, 두 관계는 서로 독립적이다, 즉 스포츠 게임 장르의 출고량과 스포츠 대회 개최 여부는 서로 연관성이 없음을 수치적으로 확인하였습니다.

요약하자면, 게임 설계를 할 때 출고량 데이터를 기반으로 다음과 같이 나왔습니다.

출시 타겟 지역은 북미와 유럽 지역이며, 게임 장르는 액션 게임 장르를 추천합니다. 또한 플랫폼은 ps3와 x360이 적절합니다.

만약, 시리즈 게임으로 출시를 한다면, 가장 빈도수가 많았던 스포츠 장르와 이에 가장 적절한 wii 플랫폼을 추천합니다.

 

 

 

GitHub - DAWUNHAN/Game-sales-Analysis: 게임 판매량을 데이터 분석한 레포지터리입니다.