[자료구조] Heap

힙 (Heap)

• 특정 목적을 위해 변형된 트리 구조.
• 최대값과 최소값을 빠르게 구하기 위한 완전 이진 트리 (완전 이진 트리는 데이터를 삽입할 때 최하단 왼쪽 노드에서 부터 차례대로 시작하는 트리)
• 배열의 경우, 최대값과 최소값을 찾으면 O(n) 이 걸림
• 힙의 경우, 최대값과 최소값을 찾으면, $O(log n)$ 이 걸림
• 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현 등에 활용됨

 

 

힙 (Heap) 구조

• 힙은 최대 힙(Max Heap)과 최소 힙(Min Heap)으로 분류 가능하다.
• 최대 힙 : 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다.
• 최소 힙 : 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 작거나 같다.
• 완전 이진 트리 형태이다.

 

 

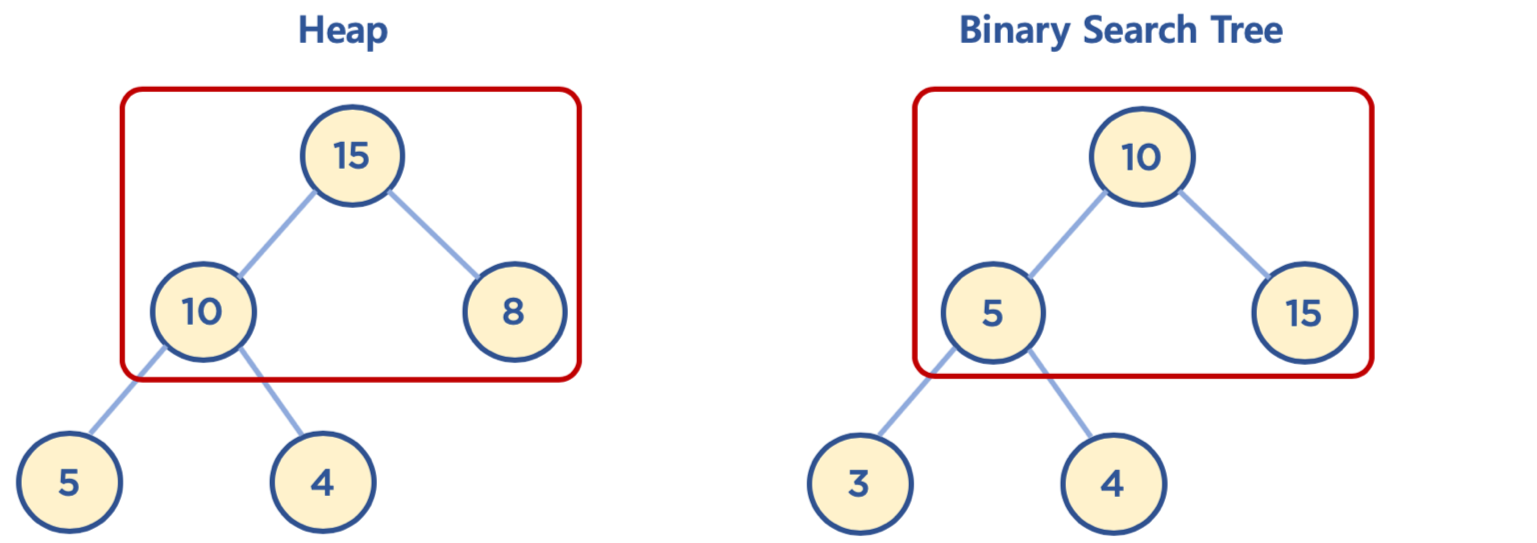
힙과 이진 탐색 트리의 공통점과 차이점

• 공통점: 둘다 이진 트리이다.
• 차이점:
  • 힙은 각 노드의 값이 자식 노드보다 크거나 같음(Max Heap의 경우)
  • 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그 다음 부모 노드, 그 다음 오른쪽 자식 노드 값이 가장 큼
  • 힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
• 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최소값 검색을 위한 구조 중 하나로 이해하면 됨

 

클래스 구현하기

• 특정 노드가 인덱스 n 일때, 자식 노드의 인덱스는 각각 2n, 2n+1 을 갖는다.
  • 그러므로 n은 1이상 이여야 하므로, 처음 힙 클래스를 만들 때 index=0은 None을 삽입한다.

class Heap:
    def __init__(self, data):
        self.heap_array = list()
        self.heap_array.append(None)
        self.heap_array.append(data)

    def move_down(self, popped_idx):
        left_child_popped_idx = popped_idx * 2
        right_child_popped_idx = popped_idx * 2 + 1

        # case1: 왼쪽 자식 노드도 없을 때
        if left_child_popped_idx >= len(self.heap_array):
            return False
        # case2: 오른쪽 자식 노드만 없을 때
        elif right_child_popped_idx >= len(self.heap_array):
            if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
                return True
            else:
                return False
        # case3: 왼쪽, 오른쪽 자식 노드 모두 있을 때
        else:
            if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
                if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
                    return True
                else:
                    return False
            else:
                if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
                    return True
                else:
                    return False

    def pop(self):
        if len(self.heap_array) <= 1:
            return None

        returned_data = self.heap_array[1]
        self.heap_array[1] = self.heap_array[-1]
        del self.heap_array[-1]
        popped_idx = 1

        while self.move_down(popped_idx):
            left_child_popped_idx = popped_idx * 2
            right_child_popped_idx = popped_idx * 2 + 1

            # case2: 오른쪽 자식 노드만 없을 때
            if right_child_popped_idx >= len(self.heap_array):
                if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
                    self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx]
                    popped_idx = left_child_popped_idx
            # case3: 왼쪽, 오른쪽 자식 노드 모두 있을 때
            else:
                if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
                    if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
                        self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx]
                        popped_idx = left_child_popped_idx
                else:
                    if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
                        self.heap_array[popped_idx], self.heap_array[right_child_popped_idx] = self.heap_array[right_child_popped_idx], self.heap_array[popped_idx]
                        popped_idx = right_child_popped_idx

        return returned_data

    def move_up(self, inserted_idx):
        if inserted_idx <= 1:
            return False
        parent_idx = inserted_idx // 2
        if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
            return True
        else:
            return False

    def insert(self, data):
        if len(self.heap_array) == 1:
            self.heap_array.append(data)
            return True

        self.heap_array.append(data)
        inserted_idx = len(self.heap_array) - 1

        while self.move_up(inserted_idx):
            parent_idx = inserted_idx // 2
            self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx]
            inserted_idx = parent_idx
        return True